مثلثاتیاسه بَرسنجی(بهانگلیسی:Trigonometry) یکی از شاخه هایریاضیاتاست که روابط میان طول اضلاع و زاویه های مثلث را مطالعه می کند. نخستین کاربرد مثلثات در مطالعاتاخترشناسیبوده است. اکنون مثلثات کاربردهای زیادی در ریاضیات محض و کاربردی دارد.
بعضی از روش های بنیادی تحلیل، مانند تبدیل فوریه و معادلات موج، از توابع مثلثاتی برای توصیف رفتار تناوبی موجود در بسیاری از فرایندهای فیزیکی استفاده می کنند. هم چنین مثلثات پایه علم نقشه برداری است.
ساده ترین کاربرد مثلثات در مثلث قائم ااویه است. هر شکل هندسی دیگری را نیز می توان به مجموعه ای از مثلث های قائم ااویه تبدیل کرد. شکل خاصی از مثلثات، مثلثات کروی است که برای مطالعه مثلثات روی سطوح کروی و منحنی به کار می رود.
تاریخچه
احتمالاً مثلثات برای استفاده درستاره شناسیایجاد شده و کاربردهای اولیه آن نیز در همین باره بوده است. ازابرخسستاره شناس یونانی به عنوان پدر مثلثات یاد می شود.
واژگان مثلثات در متون فارسی و عربی قدیم با امروزه تفاوت داشت. برخی از این تفاوت ها از این قرار است:
| نام قدیم در فارسی | معنی نام | نام امروزی |
|---|---|---|
| جیب | گریبان | سینوس |
| جیب تمام | گریبان پُر | کسینوس |
| ظل، ظل مع | سایه | تانژانت |
| ظل تمام، ظل مستوی | سایه پُر | کتانژانت |
| قاطع، قطر ظل | بُرنده | سکانت |
| قاطع تمام | بُرنده پُر | کسکانت |
کلیات
تابع های اصلی مثلثات

مجموع زاویه های داخلی مثلث برابر ۱۸۰ درجه است؛ بنابراین درمثلث قائم ااویهبا داشتن مقدار یک زاویه تند، می توان مقدار زاویه دیگر را به دست آورد. با مشخص بودن زاویه ها می توان نسبت میان اضلاع را یافت. به این ترتیب، اگر اندازه یک ضلع معلوم باشد، اندازه دو ضلع دیگر قابل محاسبه است. نسبت میان اضلاع مثلث، با استفاده از توابع مثلثاتی زیر، محاسبه می شود. در شکل روبرو، برای زاویه تندAکه مجاور وترcو ضلعbو روبرو به ضلعaاست، داریم:
- تابعسینوسکه به صورت نسبت ضلع مقابل به وتر تعریف می شود:{\displaystyle \sin A={\frac {a}{\,c\,}}}
- تابع کسینوس که به صورت نسبت ضلع مجاور به وتر تعریف می شود:{\displaystyle \cos A={\frac {b}{\,c\,}}}
- تابع تانژانت که به صورت نسبت ضلع مقابل به ضلع مجاور تعریف می شود:{\displaystyle \tan A={\frac {a}{\,b\,}}={\frac {a}{\,c\,}}*{\frac {c}{\,b\,}}={\frac {a}{\,c\,}}/{\frac {b}{\,c\,}}={\frac {\sin A}{\cos A}}\,.}
توابع مثلثاتی برای زاویهBنیز به همین ترتیب قابل محاسبه هستند. از آن جایی که ضلع مقابل زاویهAمجاور زاویهBاست و برعکس، سینوس یک زاویه برابر با کسینوس زاویه دیگر است. به عبارت دیگر:{\displaystyle \sin A=\cos B}

عکس تابع های بالا نیز با نام های سکانت (مع کسینوس)، کسکانت (مع سینوس) و کتانژانت (مع تانژانت) تعریف می شوند.
| سکانت: |
{\displaystyle \sec A={\frac {1}{\cos A}}={\frac {c}{b}}}
 |
| کسکانت: |
{\displaystyle \csc A={\frac {1}{\sin A}}={\frac {c}{a}}}
 |
| کتانژانت: |
{\displaystyle \cot A={\frac {1}{\tan A}}={\frac {\cos A}{\sin A}}={\frac {b}{a}}}
 |
دایره واحد مثلثاتی

تابع های مثلثاتی برای زاویه های تند بر اساس رابطه های بالا محاسبه می شوند. برای زاویه های بزرگتر از ۹۰ درجه (pi;/۲ رادیان)، می توان از مفهوم دایره مثلثاتی بهره گرفت. در دایره مثلثاتی، هر زاویه ای از صفر تا ۳۶۰ درجه را می توان رسم کرد و تابع های مثلثاتی آن را به دست آورد. همان گونه که در شکل روبرو دیده می شود، تابع های مثلثاتی برای زاویه های بزرگتر از ۹۰ درجه را می توان به صورت تابعی از زاویه های کوچکتر از ۹۰ درجه، یافت. برای نمونه، تابع های مثلثاتی برای زاویه های ربع دوم دایره (۹۰ تا ۱۸۰ درجه) با دوران دایره مثلثاتی به میزان ۹۰ درجه، به صورت جدول زیر به دست می آیند:
| دوران pi;/۲ |
|---|
{\displaystyle {\begin{aligned}\sin(\theta +{\tfrac {\pi }{2}})amp;=+\cos \theta \\\cos(\theta +{\tfrac {\pi }{2}})amp;=-\sin \theta \\\tan(\theta +{\tfrac {\pi }{2}})amp;=-\cot \theta \\\csc(\theta +{\tfrac {\pi }{2}})amp;=+\sec \theta \\\sec(\theta +{\tfrac {\pi }{2}})amp;=-\csc \theta \\\cot(\theta +{\tfrac {\pi }{2}})amp;=-\tan \theta \end{aligned}}} |
تناوب
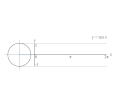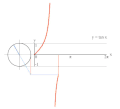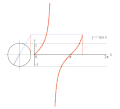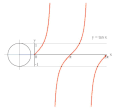
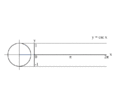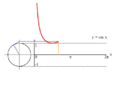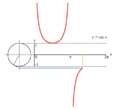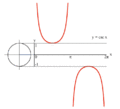
تابع های مثلثاتی برای زاویه های بزرگتر از ۳۶۰ درجه (۲pi;) و کوچکتر از صفر درجه نیز تعریف می شوند. برای هر زاویه 'theta; مقدار تابع، برابر با مقدار تابع برای زاویه theta; درون دایره (lrm;۰
تابع وارون
برای تابع های مثلثاتی، تابع وارون در بازه مشخصی کهشرط یک به یک بودنتابع برقرار باشد، تعریف می شود. این تابع ها متناظر با تابع اصلی، آرک سینوس، آرک کسینوس و آرک تانژانت نامیده می شوند.
روابط اصلی
بعضی از رابطه های مثلثاتی برای همه زاویه ها بر قرار هستند که به این رابطه ها،اتحاد مثلثاتیگفته می شود. از جمله، برخی از این اتحادها در تعیین مشخصات مثلث (مانند مساحت و شعاعدایره محیطی) کاربرد دارند و برخی برای محاسبه تابع های مثلثاتی برای مجموع یا تفاضل دو زاویه مورد استفاده قرار می گیرند.
اتحادهای فیثاغورس
اتحاد اصلی به صورت زیر است:
- {\displaystyle \sin ^{2}A+\cos ^{2}A=1\ }
می توان از اتحاد بالا دو اتحاد دیگر را استخراج نمود:
- {\displaystyle \sec ^{2}A-\tan ^{2}A=1\ }
- {\displaystyle \csc ^{2}A-\cot ^{2}A=1\ }
کاربرد اتحادها در مثلث
قانون سینوس ها
با استفاده از قانون سینوس ها در هر مثلث دلخواه، می توان با معلوم بودن اندازه یک ضلع و دو زاویه مجاور آن، اندازه دو ضلع دیگر را محاسبه نمود. هم چنین می توان مساحت مثلث (Delta;) و شعاع دایره محیطی آن (R) را به دست آورد:
- {\displaystyle {\frac {a}{\sin A}}={\frac {b}{\sin B}}={\frac {c}{\sin C}}=2R={\frac {abc}{2\Delta }}}
بر اساس اتحاد بالا، مساحت مثلث با معلوم بودن اندازه دو ضلع و زاویه میان آن ها از رابطه زیر، قابل محاسبه است:
- {\displaystyle {\mbox{Area}}=\Delta ={\frac {1}{2}}ab\sin C.}
قانون کسینوس ها[ویرایش]
با استفاده از قانون کسینوس ها در هر مثلث دلخواه، با معلوم بودن اندازه دو ضلع و زاویه میان آن ها، اندازه ضلع سوم به صورت زیر تعیین می شود:
- {\displaystyle c^{2}=a^{2}+b^{2}-2ab\cos C,\,}
رابطه های تبدیل زاویه
{\displaystyle \sin(A\pm B)=\sin A\ \cos B\pm \cos A\ \sin B}
- {\displaystyle \cos(A\pm B)=\cos A\ \cos B\mp \sin A\ \sin B}
- {\displaystyle \tan(A\pm B)={\frac {\tan A\pm \tan B}{1\mp \tan A\ \tan B}}}
- {\displaystyle \cot(A\pm B)={\frac {\cot A\ \cot B\mp 1}{\cot B\pm \cot A}}}
برخی روابط مثلثاتی
- {\displaystyle \sin(2\alpha )=2sin(\alpha )cos(\alpha )}
- {\displaystyle cos(2\alpha )=cos^{2}(\alpha )-sin^{2}(\alpha )=1/2(1-sin(2\alpha ))=1/2(1+cos(2\alpha ))}
نگارخانه
مشخصات
- انجمن ادبیات داستانی ایده
- heidar119
- shariandressshop
- partynightdressshop
- marmar78
- فروشگاه اینترنتی زیر زیر قیمت ها
- raouf1398
- .
- بلاگی برای فایل ها
- اَرْغَنوٓنْ
- refreshtip
- marketba
- saeed1991
- داستانها و نکات قرآنی
- mansari
- babagolzade
- دانلود جزوه pdf
- ubook
- پيش به سوي داشتن مدرسه اي بهتر
- چهار سوی علم
- برای مهدی
- radikal
- text021dis2006love
- 058fdffdf69iu
- 0584gfyth9iu














درباره این سایت