daneshtizhooshan
تعداد صفحات فايل:59
پروژه بررسی نظریه ولایت مطلقه فقیه درسیره امام (ره)
قيمت فايل فقط 8,000 تومان
پروژه بررسی نظریه ولایت مطلقه فقیه درسیره امام (ره)
چکیده:
مقاله نشان مىrlm;دهد <<ولایت مطلقه فقیهrlm;>> به آن مفهوم كه امامrlm;<<رضrlm;>> مد نظر داشتند، از همانrlm;ابتدا و نخستین مكتوبات ایشان، مورد توجه و اعتقاد امام بوده و چرخش و تجدید نظرى دردیدگاه ایشان واقع نشده است. مقاله، پاسخى مستدل به كسانى است كه براى نظریه ولایت فقیهrlm;و حكومت اسلامى امام، چند مرحله تجدید نظر قائل شده و ولایت مطلقه فقیه را ایدهrlm;اىrlm;خلقrlm;الساعة و شخصى خواندهrlm;اند و حتى مفهوم ولایت مطلقه را مورد تحریف قرار دادهrlm;اند.
مقدمه
پیروزى انقلاب اسلامى ایران در22 بهمن 1357، یكى ازكهنrlm;ترین نظامهاى سلطنتى راازمیان برد و برویرانهrlm;هاى سلطنت و <<اندیشه ى شاهىrlm;>>، جمهورى اسلامى رابرپایه <<نظریه ولایت مطلقه فقیهrlm;>> امامrlm;خمینى(ره) بنانهاد. نظریه ولایت فقیه، درفقه شیعى از قدمتى هزارساله برخوردار است و اگرچه درباره همه جزئیات اختیاراتrlm;ولىrlm;فقیه، اجماع نظر نبوده اما همواره از آن سخن راندهrlm;اند. امام(ره) ازكسانى است كه به تفصیل دراین بارهrlm;نظریهrlm;پردازى كردهrlm;اند. ویژگى نظریه ولایت مطلقه فقیه امام خمینى(ره)، اعتقاد ایشان به اطلاق و گستردگىrlm;اختیارات ولى فقیه و همrlm;طرازى آن بااختیارات حكومتى پیامبر(ص) و ائمه(ع) مىrlm;باشد و این نوع نگرش درتمام آثار شفاهى و مكتوب ایشان آمده است.
.
مفهوم <<ولایتrlm;>>
<<ولایتrlm;>> به معناى محبت و نصرت و یارى كردن، موضوع بحث ما نیست. محل بحث، ولایتrlm;به معناىrlm;حكومت است. در این خصوص مىrlm;توان به تعریف بحرالعلوم ازاین واژه اشاره كرد:
<<در اصطلاح، <<ولایتrlm;>> به معنى سرپرستى وسلطه داشتن برفرد یا افرادمعین مىrlm;باشد و در حقیقتrlm;بیانگرنوعى حق دخالت واعمال نظر درامرى براى شخص خاص است. مصطلح فقها آن است كه <<ولایتrlm;>> به كسرو او - سلطه برغیر به حكم عقل یا شرع، در بدن یامال و یا هر دو مىrlm;باشد. این سلطه مىrlm;تواند اصالتا یا عرضاملحوظ گردد.>> (1)
باچنین تبیینى ولایت، بیانگرقدرت تسلط و سرپرستى فرد براشخاص حقیقى یادیگر افراد است. چنینrlm;سلطهrlm;اى داراى ابعاد ومراحل مختلفى است. شرط این سلطه درتمام ابعادش، حفظ مصلحت ومنافع حقیقى وافراد تحت ولایت مىrlm;باشد.
قيمت فايل فقط 8,000 تومان
مشخصات
واژهٔزیست فناورییابیوتکنولوژی(بهفرانسوی:Biotechnologie،بیوتکنولوژی)(بهانگلیسی:Biotechnology،بایوتکنالوجی) به مفهوم استفاده از سیستم های زنده وجاندارانبرای توسعه یا تولید محصولات یا هر گونه کاربرد فناورانه که از سیستم های زیستی، جانداران یا مشتقات آن استفاده می کند تا محصولات یا فرآیندهای خاصی را ایجاد یا اصلاح نماید، به کار برده شد. به طور کلی هر گونه کنش هوشمندانه بشر در آفرینش، بهبود و عرضه فراورده های گوناگون با استفاده از جانداران، به ویژه از راه دستکاری آن ها در سطح مولکولی در حوزه این مهم ترین، پاک ترین و اقتصادی ترینفناوریحاضر یعنی زیست فناوری، قرار می گیرد. نام این دانش از این رو در ایران با نام <<بیوتکنولوژی>> شناخته می شود که تقریباً در همه کشورهای جهان با همین نام شناخته می شود.
زیست فناوری از جمله واژه های پر سرو صدای سال های اخیر است. این واژه را درست یا نادرست به مفهوم همه چیز برای مردم به کار می برند. بیوتکنولوژی را در یک تعریف کلی به کارگیریریزاندامگانیاجاندارانیافرایندهای زیستیدر صنایع تولیدی یا خدماتی دانسته اند. تعریف ساده این پدیده نوین عبارت است از دانشی که کاربرد یکپارچهزیست شیمی،میکروب شناسیو فناوری های تولید را در سامانه های زیستی به دلیل استفاده ای که در سرشت بین رشته ای علوم دارد مطالعه می کنند. در تعریف دیگر بیوتکنولوژی را چنین تشریح کرده اند:
فنونی که از موجودات زنده برای ساخت یا تغییر محصولات، ارتقا کیفی گیاهان یا حیوانات و تغییر صفاتمیکروارگانیسم هابرای کاربردهای ویژه استفاده می کنند. بیوتکنولوژی به لحاظ ویژگی های ذاتی خود دانشی بین رشته ای است. کاربرد این گونه دانش ها در مواردی است که ترکیب ایده های حاصل در طی همکاری چند رشته به تبلور قلمرویی با نظام جدید می انجامد و زمینه ها وروش شناسیخاص خود را دارد و در نهایت حاصل برهم کنش بخش های گوناگونزیست شناسیومهندت. زیست فناوری در اصل هسته ای مرکزی و دارای دو جزء است: یک جزء آن در پی دستیابی به بهترینکاتالیزوربرای یک فرایند یا عملکرد ویژه است و جزء دیگر سامانه یا واکنشگری است که کاتالیزورها در آن عمل می کنند. (بنگریدمهندسی ژنتیک،کشت سوسپانسیون سلولی،کشت سلولوفرآوری زیستی)
مشخصات
مثلثاتیاسه بَرسنجی(بهانگلیسی:Trigonometry) یکی از شاخه هایریاضیاتاست که روابط میان طول اضلاع و زاویه های مثلث را مطالعه می کند. نخستین کاربرد مثلثات در مطالعاتاخترشناسیبوده است. اکنون مثلثات کاربردهای زیادی در ریاضیات محض و کاربردی دارد.
بعضی از روش های بنیادی تحلیل، مانند تبدیل فوریه و معادلات موج، از توابع مثلثاتی برای توصیف رفتار تناوبی موجود در بسیاری از فرایندهای فیزیکی استفاده می کنند. هم چنین مثلثات پایه علم نقشه برداری است.
ساده ترین کاربرد مثلثات در مثلث قائم ااویه است. هر شکل هندسی دیگری را نیز می توان به مجموعه ای از مثلث های قائم ااویه تبدیل کرد. شکل خاصی از مثلثات، مثلثات کروی است که برای مطالعه مثلثات روی سطوح کروی و منحنی به کار می رود.
تاریخچه
احتمالاً مثلثات برای استفاده درستاره شناسیایجاد شده و کاربردهای اولیه آن نیز در همین باره بوده است. ازابرخسستاره شناس یونانی به عنوان پدر مثلثات یاد می شود.
واژگان مثلثات در متون فارسی و عربی قدیم با امروزه تفاوت داشت. برخی از این تفاوت ها از این قرار است:
| نام قدیم در فارسی | معنی نام | نام امروزی |
|---|---|---|
| جیب | گریبان | سینوس |
| جیب تمام | گریبان پُر | کسینوس |
| ظل، ظل مع | سایه | تانژانت |
| ظل تمام، ظل مستوی | سایه پُر | کتانژانت |
| قاطع، قطر ظل | بُرنده | سکانت |
| قاطع تمام | بُرنده پُر | کسکانت |
کلیات
تابع های اصلی مثلثات

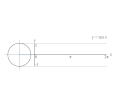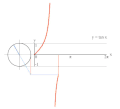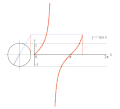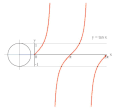
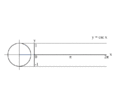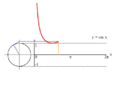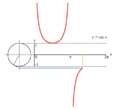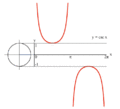
مجموع زاویه های داخلی مثلث برابر ۱۸۰ درجه است؛ بنابراین درمثلث قائم ااویهبا داشتن مقدار یک زاویه تند، می توان مقدار زاویه دیگر را به دست آورد. با مشخص بودن زاویه ها می توان نسبت میان اضلاع را یافت. به این ترتیب، اگر اندازه یک ضلع معلوم باشد، اندازه دو ضلع دیگر قابل محاسبه است. نسبت میان اضلاع مثلث، با استفاده از توابع مثلثاتی زیر، محاسبه می شود. در شکل روبرو، برای زاویه تندAکه مجاور وترcو ضلعbو روبرو به ضلعaاست، داریم:
- تابعسینوسکه به صورت نسبت ضلع مقابل به وتر تعریف می شود:{\displaystyle \sin A={\frac {a}{\,c\,}}}
- تابع کسینوس که به صورت نسبت ضلع مجاور به وتر تعریف می شود:{\displaystyle \cos A={\frac {b}{\,c\,}}}
- تابع تانژانت که به صورت نسبت ضلع مقابل به ضلع مجاور تعریف می شود:{\displaystyle \tan A={\frac {a}{\,b\,}}={\frac {a}{\,c\,}}*{\frac {c}{\,b\,}}={\frac {a}{\,c\,}}/{\frac {b}{\,c\,}}={\frac {\sin A}{\cos A}}\,.}
توابع مثلثاتی برای زاویهBنیز به همین ترتیب قابل محاسبه هستند. از آن جایی که ضلع مقابل زاویهAمجاور زاویهBاست و برعکس، سینوس یک زاویه برابر با کسینوس زاویه دیگر است. به عبارت دیگر:{\displaystyle \sin A=\cos B}

عکس تابع های بالا نیز با نام های سکانت (مع کسینوس)، کسکانت (مع سینوس) و کتانژانت (مع تانژانت) تعریف می شوند.
| سکانت: |
{\displaystyle \sec A={\frac {1}{\cos A}}={\frac {c}{b}}}
 |
| کسکانت: |
{\displaystyle \csc A={\frac {1}{\sin A}}={\frac {c}{a}}}
 |
| کتانژانت: |
{\displaystyle \cot A={\frac {1}{\tan A}}={\frac {\cos A}{\sin A}}={\frac {b}{a}}}
 |
دایره واحد مثلثاتی

تابع های مثلثاتی برای زاویه های تند بر اساس رابطه های بالا محاسبه می شوند. برای زاویه های بزرگتر از ۹۰ درجه (pi;/۲ رادیان)، می توان از مفهوم دایره مثلثاتی بهره گرفت. در دایره مثلثاتی، هر زاویه ای از صفر تا ۳۶۰ درجه را می توان رسم کرد و تابع های مثلثاتی آن را به دست آورد. همان گونه که در شکل روبرو دیده می شود، تابع های مثلثاتی برای زاویه های بزرگتر از ۹۰ درجه را می توان به صورت تابعی از زاویه های کوچکتر از ۹۰ درجه، یافت. برای نمونه، تابع های مثلثاتی برای زاویه های ربع دوم دایره (۹۰ تا ۱۸۰ درجه) با دوران دایره مثلثاتی به میزان ۹۰ درجه، به صورت جدول زیر به دست می آیند:
| دوران pi;/۲ |
|---|
{\displaystyle {\begin{aligned}\sin(\theta +{\tfrac {\pi }{2}})amp;=+\cos \theta \\\cos(\theta +{\tfrac {\pi }{2}})amp;=-\sin \theta \\\tan(\theta +{\tfrac {\pi }{2}})amp;=-\cot \theta \\\csc(\theta +{\tfrac {\pi }{2}})amp;=+\sec \theta \\\sec(\theta +{\tfrac {\pi }{2}})amp;=-\csc \theta \\\cot(\theta +{\tfrac {\pi }{2}})amp;=-\tan \theta \end{aligned}}} |
تناوب
تابع های مثلثاتی برای زاویه های بزرگتر از ۳۶۰ درجه (۲pi;) و کوچکتر از صفر درجه نیز تعریف می شوند. برای هر زاویه 'theta; مقدار تابع، برابر با مقدار تابع برای زاویه theta; درون دایره (lrm;۰
تابع وارون
برای تابع های مثلثاتی، تابع وارون در بازه مشخصی کهشرط یک به یک بودنتابع برقرار باشد، تعریف می شود. این تابع ها متناظر با تابع اصلی، آرک سینوس، آرک کسینوس و آرک تانژانت نامیده می شوند.
روابط اصلی
بعضی از رابطه های مثلثاتی برای همه زاویه ها بر قرار هستند که به این رابطه ها،اتحاد مثلثاتیگفته می شود. از جمله، برخی از این اتحادها در تعیین مشخصات مثلث (مانند مساحت و شعاعدایره محیطی) کاربرد دارند و برخی برای محاسبه تابع های مثلثاتی برای مجموع یا تفاضل دو زاویه مورد استفاده قرار می گیرند.
اتحادهای فیثاغورس
اتحاد اصلی به صورت زیر است:
- {\displaystyle \sin ^{2}A+\cos ^{2}A=1\ }
می توان از اتحاد بالا دو اتحاد دیگر را استخراج نمود:
- {\displaystyle \sec ^{2}A-\tan ^{2}A=1\ }
- {\displaystyle \csc ^{2}A-\cot ^{2}A=1\ }
کاربرد اتحادها در مثلث
قانون سینوس ها
با استفاده از قانون سینوس ها در هر مثلث دلخواه، می توان با معلوم بودن اندازه یک ضلع و دو زاویه مجاور آن، اندازه دو ضلع دیگر را محاسبه نمود. هم چنین می توان مساحت مثلث (Delta;) و شعاع دایره محیطی آن (R) را به دست آورد:
- {\displaystyle {\frac {a}{\sin A}}={\frac {b}{\sin B}}={\frac {c}{\sin C}}=2R={\frac {abc}{2\Delta }}}
بر اساس اتحاد بالا، مساحت مثلث با معلوم بودن اندازه دو ضلع و زاویه میان آن ها از رابطه زیر، قابل محاسبه است:
- {\displaystyle {\mbox{Area}}=\Delta ={\frac {1}{2}}ab\sin C.}
قانون کسینوس ها[ویرایش]
با استفاده از قانون کسینوس ها در هر مثلث دلخواه، با معلوم بودن اندازه دو ضلع و زاویه میان آن ها، اندازه ضلع سوم به صورت زیر تعیین می شود:
- {\displaystyle c^{2}=a^{2}+b^{2}-2ab\cos C,\,}
رابطه های تبدیل زاویه
{\displaystyle \sin(A\pm B)=\sin A\ \cos B\pm \cos A\ \sin B}
- {\displaystyle \cos(A\pm B)=\cos A\ \cos B\mp \sin A\ \sin B}
- {\displaystyle \tan(A\pm B)={\frac {\tan A\pm \tan B}{1\mp \tan A\ \tan B}}}
- {\displaystyle \cot(A\pm B)={\frac {\cot A\ \cot B\mp 1}{\cot B\pm \cot A}}}
برخی روابط مثلثاتی
- {\displaystyle \sin(2\alpha )=2sin(\alpha )cos(\alpha )}
- {\displaystyle cos(2\alpha )=cos^{2}(\alpha )-sin^{2}(\alpha )=1/2(1-sin(2\alpha ))=1/2(1+cos(2\alpha ))}
نگارخانه
مشخصات
- انجمن ادبیات داستانی ایده
- heidar119
- shariandressshop
- partynightdressshop
- marmar78
- فروشگاه اینترنتی زیر زیر قیمت ها
- raouf1398
- .
- بلاگی برای فایل ها
- اَرْغَنوٓنْ
- refreshtip
- marketba
- saeed1991
- داستانها و نکات قرآنی
- mansari
- babagolzade
- دانلود جزوه pdf
- ubook
- پيش به سوي داشتن مدرسه اي بهتر
- چهار سوی علم
- برای مهدی
- radikal
- text021dis2006love
- 058fdffdf69iu
- 0584gfyth9iu















درباره این سایت